2 Drawing from Densities

2.1 Pseudo-Random Numbers from Uniform Distribution

2.2 Inverse Transform Method

\[ \begin{aligned} F_X(x) &= \Pr \left(X \le x \right) \\ &= \Pr \left(T(U) \le x \right) \\ &= \Pr \left(U \le T^{-1}(x) \right) \\ &= T^{-1}(x) \end{aligned} \]

2.3 Example: Exponential

\[ F(y,\lambda) = 1 - \exp\left( -\lambda y \right) \hspace{1em} \text{for} \ y \ge 0 \]

\[ F^{-1}(u) = -\log(1-u) / \lambda \]

n <- 1e4
lambda <- 0.3
u <- runif(n)
y <- -log(1-u)/lambda

x <- seq(from=0, to=ceiling(max(y)), length.out=100)
hist(y, freq=F, breaks=100)
lines(x=x, y=dexp(x,lambda), lwd=2)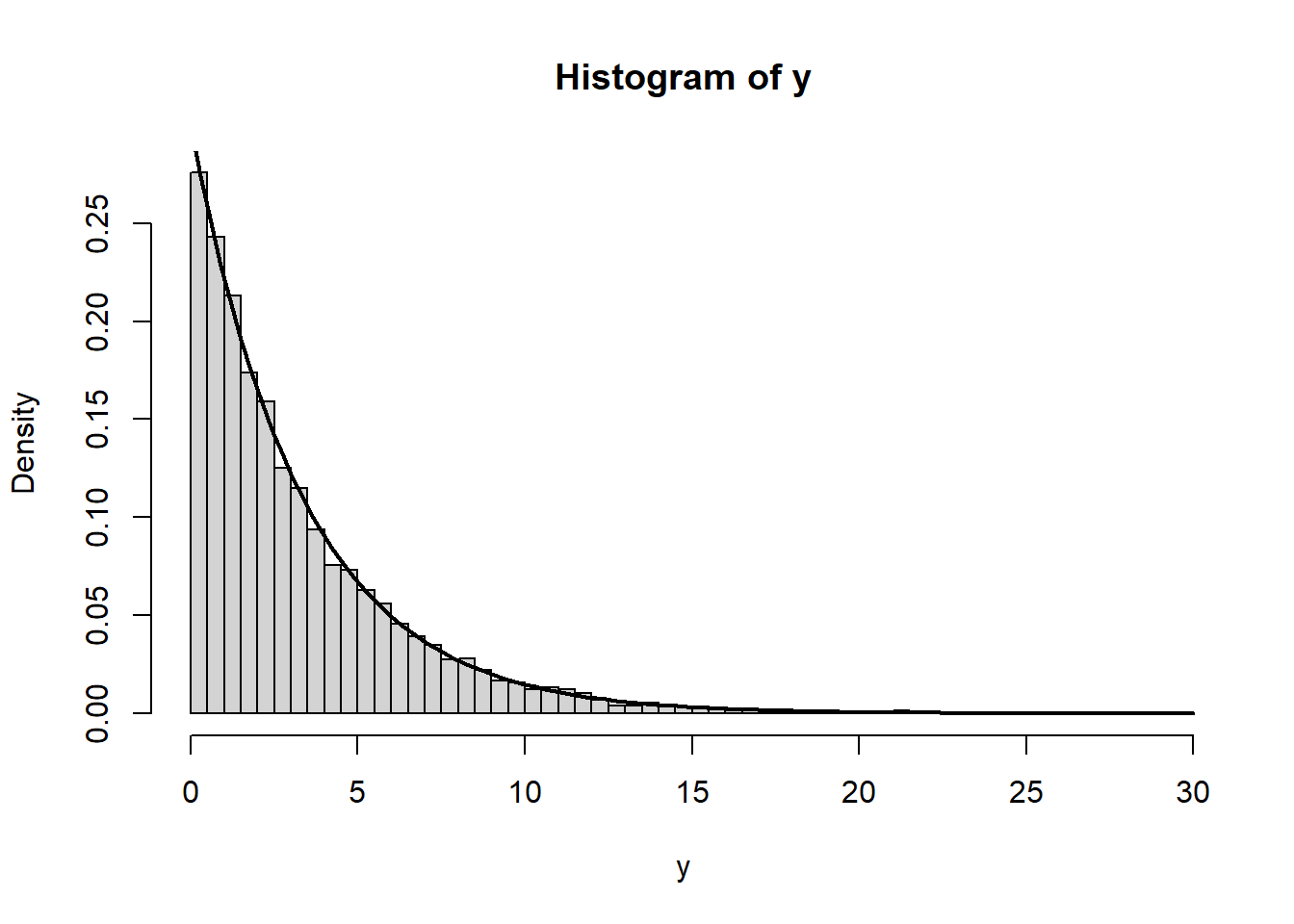

2.4 Example: Gumbel

\[ F(y) = \exp \left( -\exp \left( -y \right) \right) \]

\[ F^{-1}(u) = -\log(-log(u)) \]

n <- 1e4
u <- runif(n)
y <- -log(-log(u))

x <- seq(from=-3, to=ceiling(max(y)), length.out=500)
hist(y, freq=F, breaks=100)
lines(x=x, y=ordinal::dgumbel(x), lwd=2)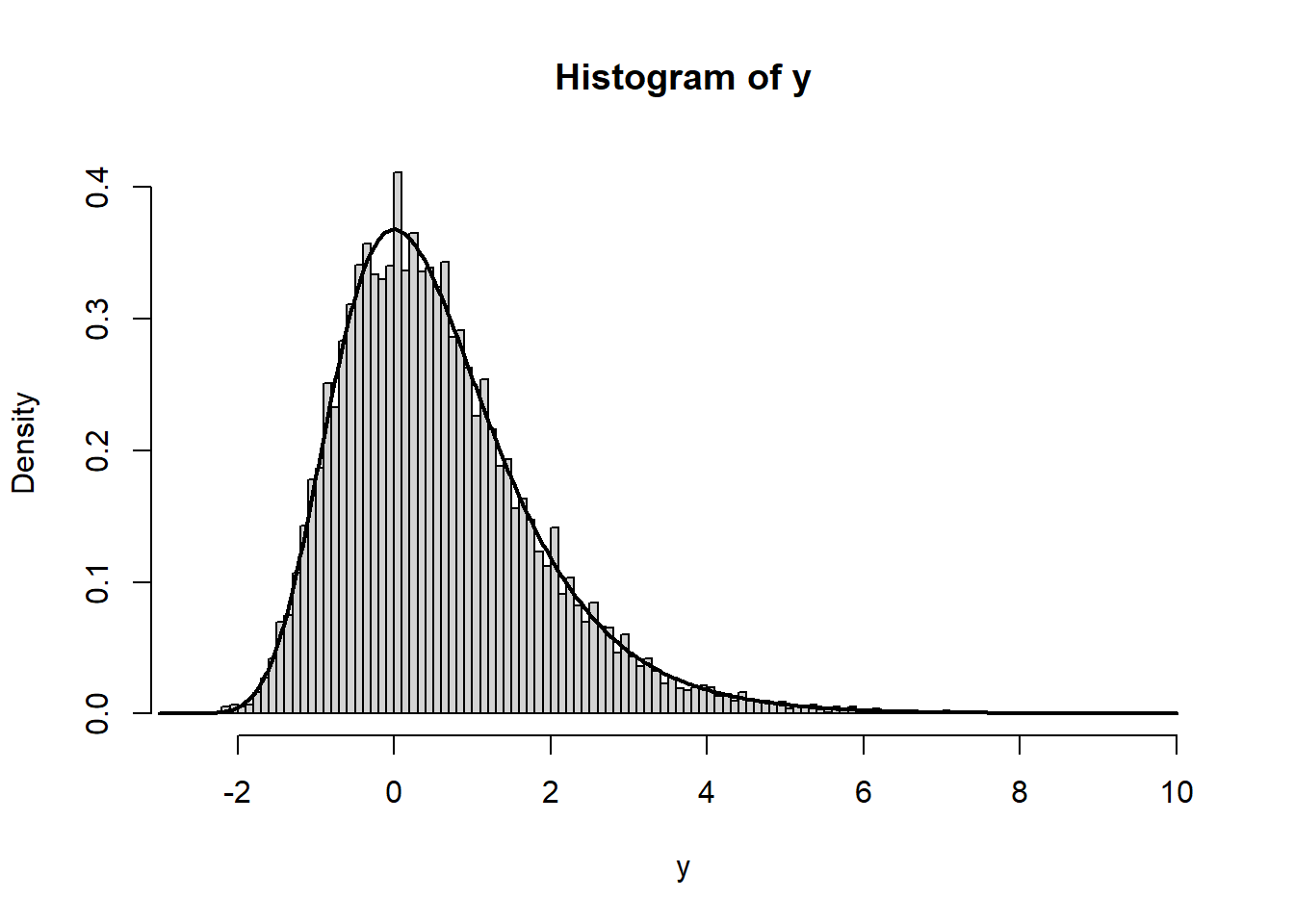

2.5 Example: Logistic

\[ F(y) = \frac{1}{1+\exp \left( -x \right)} \]

\[ F^{-1}(u) = \log(u) - \log(1-u) \]

n <- 1e4
u <- runif(n)
y <- log(u) - log(1-u)

x <- seq(from=floor(min(y)), to=ceiling(max(y)), length.out=500)
hist(y, freq=F, breaks=100)
lines(x=x, y=dlogis(x), lwd=2)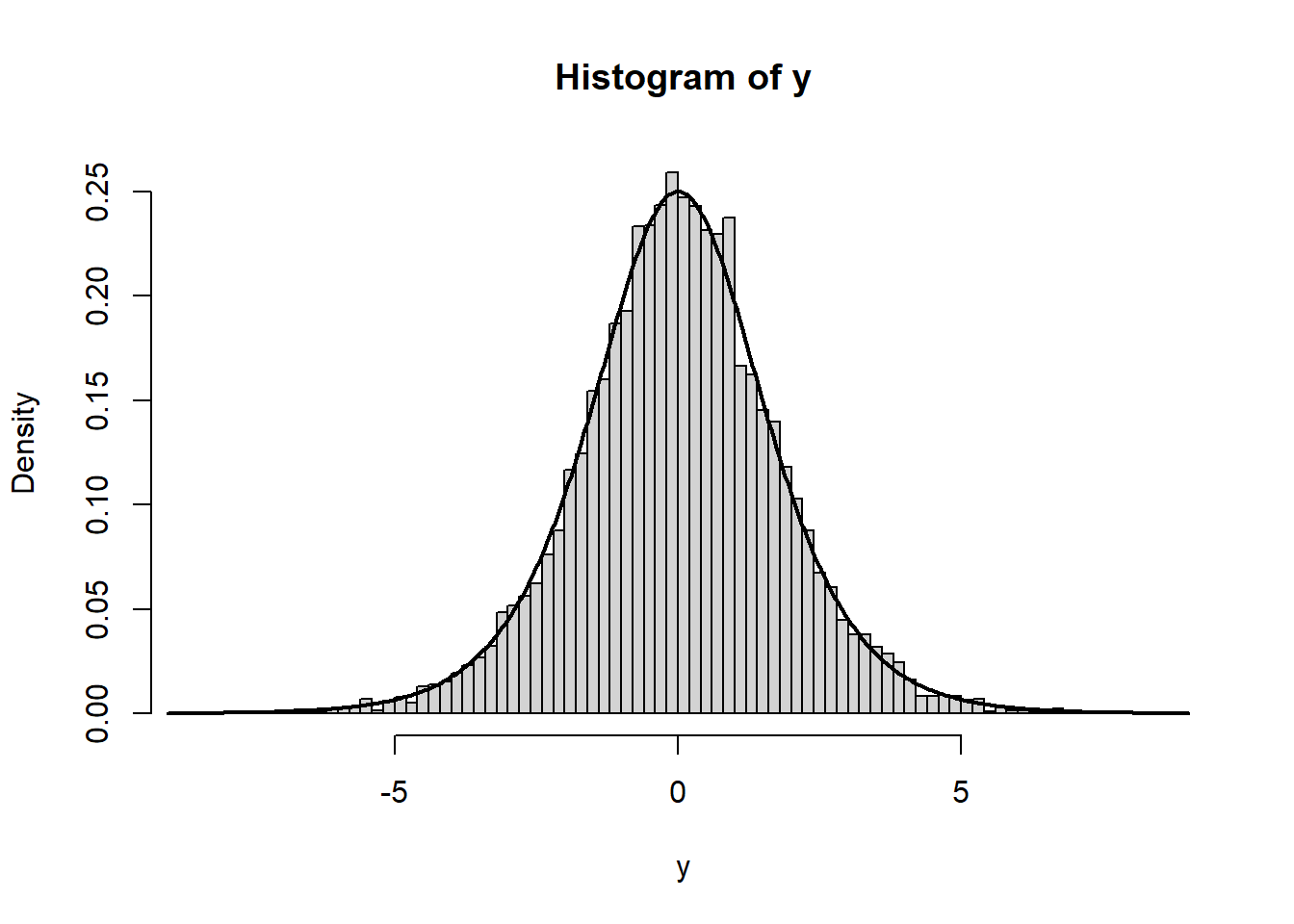

2.6 Example: Normal

n <- 1e4
y <- rnorm(n)

u <- runif(n)
y <- qnorm(u)